原文: Index 1,600,000,000 Keys with Automata and Rust
看上去有限状态机在除了表达式计算之外的一些事情上也很有用。有限状态机也可以用来压缩表示有序集合或者字符串映射,并且能够非常快的在上面进行检索。
在这篇文章里,我会告诉你如何用有限状态机作为表示有序集合和映射的数据结构。包括介绍一个Rust的实现:fst。它包含完整的API文档。我也会展示给你如何用一个简单的命令行工具来构建他们。最后,我会以讨论几个索引16亿条July 2015 Common Crawl Archive网址的实验
这篇文章展示的技术也是Lucene用来表示部分倒排索引的方法。
在这个过程中,我们会谈到内存映射,自动机和正则匹配,Levenshtein距离下的模糊检索和流式集合操作。
目标读者: 熟悉编程和基础的数据结构。不要求有自动机理论或者Rust的经验。
预告片
作为预告,我们先展示一下我们的成果。我们先快速看一个例子。我们先不看16亿字符串,我们先考虑1600w维基百科文章标题(384M)。这是我们用来索引他们的方法:
$ time fst set --sorted wiki-titles wiki-titles.fst
real 0m18.310
最终的索引wiki-titles.fst是157M。作为比较,gzip花了12秒并且压缩到了91m。 (对于某些数据集,我们的编码方式可以同时在速度和压缩率上超过gzip)。
然而,这是一些gzip做不了的事情:快速找到所有以Homer the开头的文章标题:
$ time fst grep wiki-titles.fst 'Homer the.*'
Homer the Clown
Homer the Father
Homer the Great
Homer the Happy Ghost
Homer the Heretic
Homer the Moe
Homer the Smithers
...
real 0m0.023s
作为比较,grep 在原始未压缩的数据上用了0.3秒。
最后,来一些grep也做不了的事情,快速找到所有和Homer Simpson差距在一定编辑距离内的文章标题:
$ time fst fuzzy wiki-titles.fst --distance 2 'Homer Simpson'
Home Simpson
Homer J Simpson
Homer Simpson
Homer Simpsons
Homer simpson
Homer simpsons
Hope Simpson
Roger Simpson
real 0m0.094s
这篇文章非常的长,所以如果你只是来看个热闹,那么你可以直接跳到我们索引16亿键的部分。
目录
这个文章非常长,所以我把目录放在这里以便于你们想要跳过某些内容。
第一部分简单的介绍一下有限状态机,以及把它用作数据结构。这一章是为了给你一个关于这个数据结构的基本印象。这一章没有代码。
第二部分采用了第一章的抽象,并且展示了一个它的实现。这一章主要是为了展示如果用我的fst。这一章有代码。我们会讨论一些实现细节,但是会避免细枝末节。如果你不在意代码而只想看看真实数据上的效果,完全可以跳过这一章。
第三章和最后一张展示了如何用简单的命令行工具构建索引。我们会看一些真实的数据集,并且尝试展示出把有限状态机作为数据结构的性能因素。
数据结构: 有限自动机
有限自动机是一个状态的集合和从一个状态转变到另一个状态的变化集合。有一个状态被标记为起始状态,0个或多个状态被标记为终止状态。一个有限状态机每个时间总是只在一个状态。
有限状态机非常的通用并且可以用来给一系列的过程建模。比如,考虑我家猫Cauchy的一天:
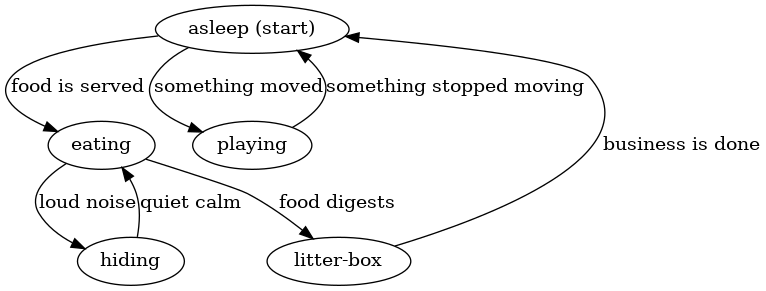
这里有一些状态"睡眠"或者“吃饭”还有一些变化例如“食物已经准备好了”或者“有东西移动了”。显然,这里不会有任何的终止状态。
注意到,有限状态机近似地描述了我们现实中的概念。Cauchy不能同时在玩和在睡觉,所以它满足了我们状态机在一个时间只处在一个状态的条件。另外,从一个状态变化到另一个状态的条件只要求了环境中的一个输入。也就是说,在睡觉这个状态没有携带它是玩累了转变来的还是吃饱了心满意足过来的。不过Cauchy怎么入睡的,他总是会起来如果听到了有东西在动的声音或者晚餐铃响了。
Cauchy的有限状态机可以针对一系列输入进行计算。例如,考虑如下输入:
- 食物准备好了
- 大的噪音
- 安静
- 食物消化
如果我们把这些输入应用到上面的机器中去,那么Cauchy会按顺序在以下几个状态中变化: 睡觉,吃东西,躲起来,吃东西,小盒子。 因此,如果我们观察到食物准备好了,紧接着有一声大响,然后安静下来,最后Cauchy消化了食物,那么我们可以得到结论,Cauchy现在在她的小盒子里。
这个愚蠢的例子展示了通常的有限自动机是什么样子。但对于我们来说,为了实现有序集合和映射的数据结构,我们需要再有限状态机上添加一些限制。
有序集合
一个有序集合就像一个普通的集合,除了它的键是有序的。也就是说,一个有序集合提供了一个有序迭代器来遍历它的键。通常来说,一个有序集合是通过一个二叉搜索树或者一个btree来实现的,而一个无序集合是通过哈希表来实现的。在我们的例子里,我们会看到一个使用 deterministic acyclic finite state acceptor确定无环有限状态接收器 (缩写 FSA)。
一个确定无环有限状态接收器是一个满足如下条件的有限状态机:
- 确定性的。这是指在任意状态下,对于任意的输入,只有最多一个变化可以产生。
- 无环。这意味着不能去访问一个已经访问过的状态。
- 一个接收器。这意味着这个有限状态机接受特定序列的输入,当且仅当在这一系列输入的末尾停留在终止状态。(这个条件和前两个条件不一样的地方在于,在下一章有序映射的时候会改变)
我们怎么用这些特性来表示一个集合呢?关键是在机器的变化上存储我们集合的键。通过这种方式,任意给一串输入(即字符),我们能够通过评估这个FSA是否在终止态上结束来知道这个键是不是在集合里。
考虑这个只有一个键“jul”的集合,对应的FSA长这样:

考虑如果我们询问FSA是否包含键“jul”时会发生什么?我们需要按顺序去处理字符:
- 给定j,FSA从起始状态0移动到1。
- 给定u,FSA从1移动到2。
- 给定l,FSA从2移动到3。
因为键的所有成员都已经被塞给了FSA,现在我们能问,FSA是在最终状态了吗?确实是(注意状态3是个双圆环),所以我们能说jul是在集合里的。
考虑如果我们来测试一个不在集合里的键会发生什么。例如,jun:
- 给定j,FSA从起始状态0移动到1。
- 给定u,FSA从1移动到2。
- 给定n,FSA不能移动,流程停止。
FSA不能移动因为从状态2唯一移动出去的输入是l,但是当前的输入是n。因为 l != n,所以FSA不能按照这个输入来变化。既然FSA按照给定的输入不能移动了,我们可以得到结论,这个键不在集合中。我们也不用去处理后面的输入了。
考虑另外一个键,ju:
- 给定j,FSA从起始状态0移动到1。
- 给定u,FSA从1移动到2。
在这个例子里,全部的输入都已经给完了而FSA还在状态2.要决定ju是不是在集合里,必须要问2是不是一个终止状态。既然2不是,那么我们就可以说,ju这个键不在集合里了。
这里需要指出的是,用来确认一个键在不在集合中的步数取决于键中的字符数。也就是,用来查询一个键的时间和集合的大小无关。
让我们往集合里添加另外一个键来看看会变成什么样子。下面这个FSA表示了一个包含键jul和mar的有序集合:
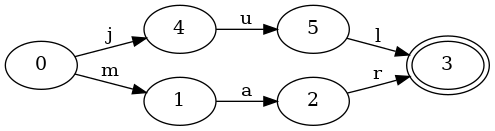
这个FSA变得有一点点复杂。初始状态0现在有了两个变化:j和 m。因此,如果给定键mar,它会首先按照m的变化进行。
这里还需要指出另外一个很重要的地方。状态3是被键jul和mar共享的。也就是说,状态3有两个变化可以到达它,j和 r。状态的共享非常重要,因为它能让我们用更小的空间存储更多的信息。
让我们看看如果我们加上jun到集合里会发生什么,它和jul含有相同的前缀。
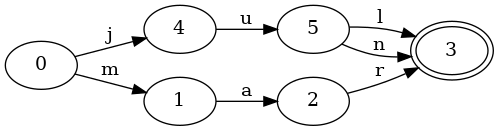
看到区别了吗?这里只有很小的变化。这个FSA看起来非常像前面那个。这里只有一个区别:加上了一个从状态5到状态3的新变化n。请注意,这个FSA没有新的状态!因为jun和jul共享了相同的前缀ju, 这些状态可以被所有的键复用。
让我们稍微改变一点点,来看看有这些键的一个集合:october, november 和 december:

既然所有三个键都共享相同的后缀ber,它只被编入FSA一次。 其中两个key共享一个稍微大一些的后缀ember,它也只被编入了FSA一次。
在我们继续看有序映射之前,我们需要花一些时间来说服自己这确实是一个有序集合。也就是说,给定一个FSA,我们怎么迭代集合里的键呢?
为了演示这个,让我们用之前构建的那个包含jul, jun 和 mar的集合:

我们可以通过按照字母顺序来遍历FSA的变化,从而枚举集合里所有的键。 例如:
- 从状态0开始,
key是空的。 - 移动到状态4,把
j加到key里。 - 移动到状态5,把
u加到key里。 - 移动到状态3,把
l加到key里。输出jul。 - 回到状态5,从
key里去掉l。 - 移动到状态3,把
n加到key里。输出jun。 - 回到状态5,从
key里去掉n。 - 回到状态4,从
key里去掉u。 - 回到状态0,从
key里去掉j。 - 移动到状态1,把
m加到key里。 - 移动到状态2,把
a加到key里。 - 移动到状态3,把
r加到key里。输出mar。
这个算法可以通过一个待访问状态的栈和一个已经访问过的变化来很直观的实现。这个算法的时间复杂度是O(n),n是集合里键的数目。空间复杂度是O(k),k是这个集合里最长的键的大小。
有序映射
和有序集合一样,一个有序映射就像一个普通的映射,但是映射的键是有良好的顺序定义的。就和集合一样,有序映射通常通过一个有序二叉树或者btree来实现,而无序映射通过哈希表来实现。在我们的例子里,我们会看到一个通过deterministic acyclic finite state transducer 确定无环有限状态转换器 (缩写FST)。
一个确定无环有限状态转换器是一个有以下特点的有限状态机(前面两个标准和前一章相同):
- 确定性的。这是指在任意状态下,对于任意的输入,只有最多一个变化可以产生。
- 无环。这意味着不能去访问一个已经访问过的状态。
- 一个转换器。意思是这个有限状态机会根据特定的一系列输入来输出相关联的值。当且仅当这一系列输入会使状态机进到终止状态。
也就是说,一个FST就像一个FSA一样,但它对于给定的键不会回答"是或者否",而是会回答“否”或者“是的,这是这个键对应的值”。
在前面一章里,表示一个集合只要求在状态机的变化中存储键。状态机接受一个输入序列,当且仅当这个序列表示的键在集合里。在这个例子里,映射需要比接受一个输入多做一点事情,它还需要返回键所关联的值。
一个关联键值对的方法是在每个变化上都附加一些数据。就像输入序列被用来把状态机从一个状态转移到另一个状态,一个输出序列也可以通过状态在状态间转移来产生。这个额外的能力让状态机成为了转换器。
让我们来看一下一个只含有一个元素的映射,jul,关联的值是7。

这个状态机和对应的集合一样,除了第一个从状态0转移到状态1的变化多了一个关联的输出7。对于其他变化,u和l其实也有输出0和他们关联在一起,但是没有在图上展示出来。
和集合一样,我们可以问这个映射是否包含键jul。但我们也需要返回输出。这是这个状态机在查找jul时处理键的过程:
- 初始化
value为0。 - 给定
j,FST从起始状态0移动到1,给value加7。 - 给定
u,FST从状态1移动到状态2,给value加0。 - 给定
l,FST从状态2移动到状态3,给value加0。
既然所有的输入都被喂给了FST,我们现在能问:这个FST到终止状态了吗?是的,所以我们能知道jul在映射里。另外,我们还知道value就是和键jul关联的值,7。
并不神奇,对吗?这个例子太简单了。一个只有一个键的映射不是特别说明问题。让我们看看当我们加上mar,关联值3,到映射里会怎么样。
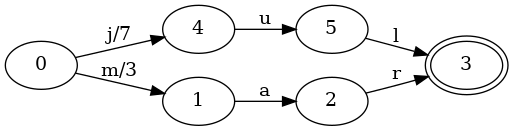
初始状态多了一个转移m和一个输出3。如果我们查找键jul,那么过程会和前面的映射一样,我们会得到值7。如果我们查找键mar,那么过程会像这样:
- 初始化
value为0。 - 给定
m,FST从起始状态0移动到1,给value加3。 - 给定
a,FST从状态1移动到状态2,给value加0。 - 给定
r,FST从状态2移动到状态3,给value加0。
这里唯一的变化在于,除了不同的输入, 在第一步的变化上加上了值3。因为所有的后续移动都只在value上加0,状态机会输出和mar关联的值是3。
让我们继续,如果我们有一些有相同前缀的键怎么样?考虑和上面一样的映射,但是加上了键jun并且关联值6:
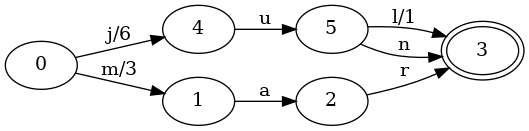
和集合一样,多添加了一个变化从状态5到状态3的变化n。但是这里还有2个不一样的地方:
- 对于输入j的从0到4的变化,它的输出从7变成了6。
- 对于输入l的从5到3的变化,它的输出从0变成了1。
这些在输出上的改变非常重要,因为这使得查找键jul对应的值时,一些细节发生了变化:
- 初始化
value为0。 - 给定
j,FST从起始状态0移动到4,给value加6。 - 给定
u,FST从状态4移动到状态5,给value加0。 - 给定
l,FST从状态5移动到状态3,给value加1。
最终的值还是7,但是我们得到这个值的方法不一样。之前是在j的变化时直接加7,现在我们只加了6,然后在最后l的变化时额外加1.
我们也应该说服自己查找键jun也是正确的:
- 初始化
value为0。 - 给定
j,FST从起始状态0移动到4,给value加6。 - 给定
u,FST从状态4移动到状态5,给value加0。 - 给定
n,FST从状态5移动到状态3,给value加0。
第一个变化给value加上了6,但在后面变化中,我们再也没有加过比0大的数了。这是因为键jun没有像jul那样经过最后的l变化。通过这种方式,所有的键都有不同的值,但是我们在有相同前缀的键之间共享了很多的数据结构。
事实上,最关键的让我们能够做到这种共享的地方在于,每一个键在整个状态机里都对应一个独一无二的路径。因此,对于每一个键来说,都能找到一个独特的变化组合。我们需要做的只是找出来如何在这些变化上安排我们的输出。(我们会在下一章看到应该怎么做。)
输出共享对相同前缀,相同后缀都成立。考虑键tuesday和thursday,分别关联值3和5(对应一个星期的天数,从周日开始)。

两个键都有相同的前缀t和一个相同的后缀sday。注意这些和键关联的值在加法层面上也是有共同前缀的。也就是说,3可以写成3+0而5可以写成3+2。这点也在状态机中体现了出来。共同前缀t有输出3。而h变化(在tuesday中没有)关联的输出是2。也就是说,当查找键tuesday时,第一个t上的值会被输出,但是后续的h变化不会,所以关联的2也不会被输出。剩下的变化都只有输出0,这些都不会改变最终返回的value。
通过我们描述的这种方法,输出看上去似乎限制很大。如果他们不是整数怎么办?事实上,在FST中可以使用的输出要求必须支持以下几种操作:
- 加法
- 减法
- 前缀 (即,找出两个输出的共同前缀)
输出必须有个加法独立元I,使得以下定律成立:
- x + I = x
- x - I = x
- prefix(x, y) = I 当
x和y没有相同前缀时。
整数显然满足这些条件(prefix的定义就是min),除此之外还有一个好处就是他们很小。其他类型可以做到满足这些条件,但目前为止,我们只支持整数。
在上面的例子里,我们只需要用到加法,但是我们在构建一个FST时,我们会需要另外两个操作。我们接下来会说到这些。